Finlandesa resolve problema matemático que desafiou cientistas por 40 anos
Ana Barros 
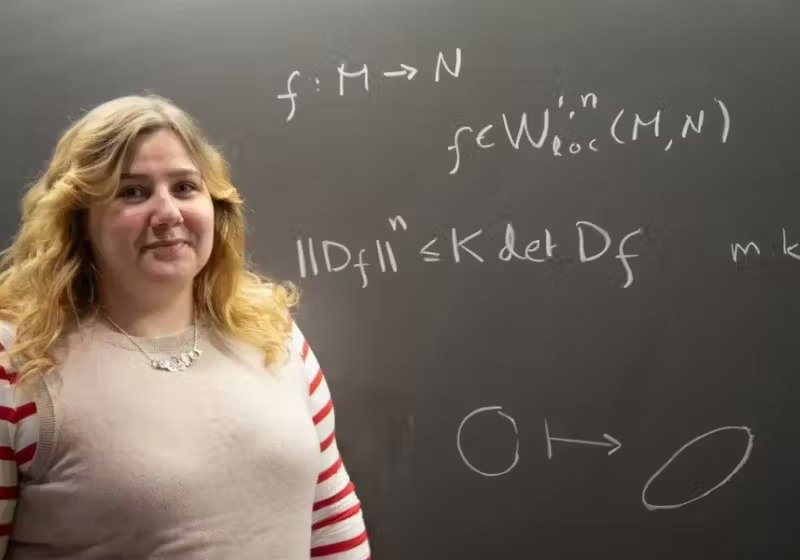
A abordagem inovadora da pesquisadora envolveu um recurso pouco convencional: o tricô.
A estudante de doutorado Susanna Heikkilä, da Universidade de Helsinque, conquistou um feito notável ao solucionar um problema matemático que permaneceu sem resposta por quatro décadas. Seu estudo, que esclarece uma questão levantada pelo matemático Misha Gromov em 1981, foi publicado no renomado Annals of Mathematics, um dos periódicos mais prestigiados do mundo.
O enigma de 1981
Há mais de 40 anos, Misha Gromov propôs uma questão fundamental sobre variedades quadridimensionais, levantando a dúvida sobre a possibilidade de mapear tais estruturas sem obstruções geométricas. O problema intrigou matemáticos por décadas, e, em 2019, Eden Prywes demonstrou que não havia uma solução simples. No entanto, foi Susanna quem conseguiu fornecer a resposta definitiva.
Tricô para entender a matemática
A abordagem inovadora da pesquisadora envolveu um recurso pouco convencional: o tricô. Durante sua apresentação, ela utilizou uma peça de tricô para representar visualmente os mapeamentos quasiregulares, ajudando a ilustrar sua teoria. Com remendos coloridos e padrões geométricos, ela demonstrou como a estrutura das variedades pode ser deformada sem perder suas propriedades essenciais.
“O principal resultado da minha tese complementa a resposta à pergunta de Gromov, permitindo classificar variedades quadridimensionais fechadas e simplesmente conectadas para as quais há um mapeamento quasiregular de um espaço euclidiano”, explicou Susanna.
Reconhecimento internacional
O impacto da descoberta foi imediato, rendendo à cientista premiações da Associação Acadêmica de Matemática e Ciências Naturais da Finlândia, além de reconhecimento de grandes agências internacionais.
O talento de Susanna foi identificado ainda no ensino médio por um professor que a incentivou a seguir na matemática. Mais tarde, durante um curso de topologia, ela se apaixonou pela área e decidiu dedicar sua carreira à pesquisa. Agora, como pós-doutoranda, Susanna continua suas investigações sobre mapeamentos e curvas quasiregulares.
Seu trabalho não apenas resolve um problema histórico, mas também abre caminho para novas descobertas na matemática e inspira futuras gerações de cientistas.
Redação 
